選択した画像 Y=ax2 グラフ 変域 252193-Y=ax2 グラフ 変域
関数の変域 まなびの学園
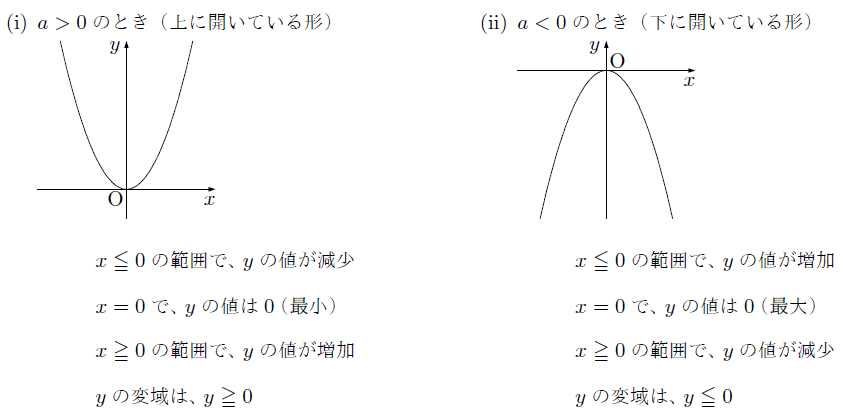
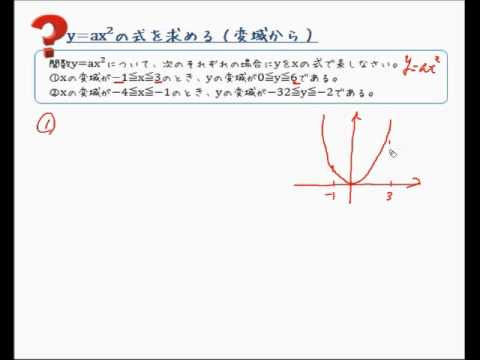
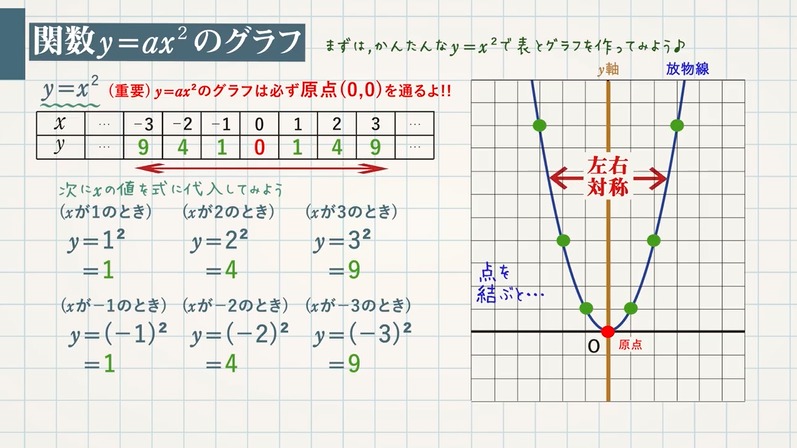
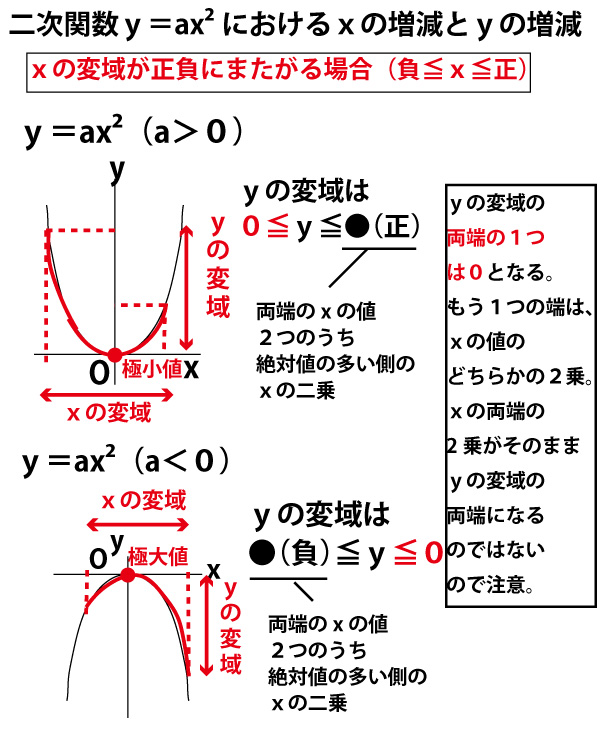
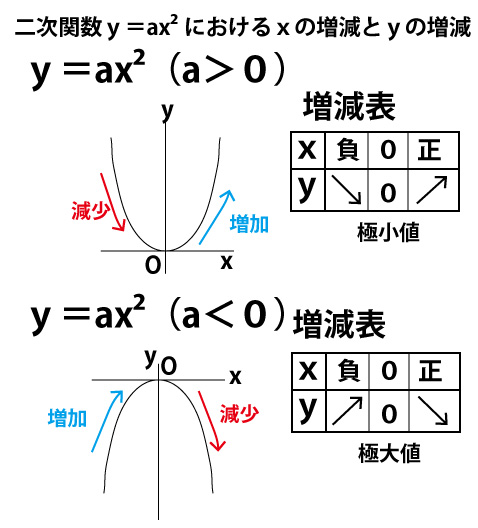
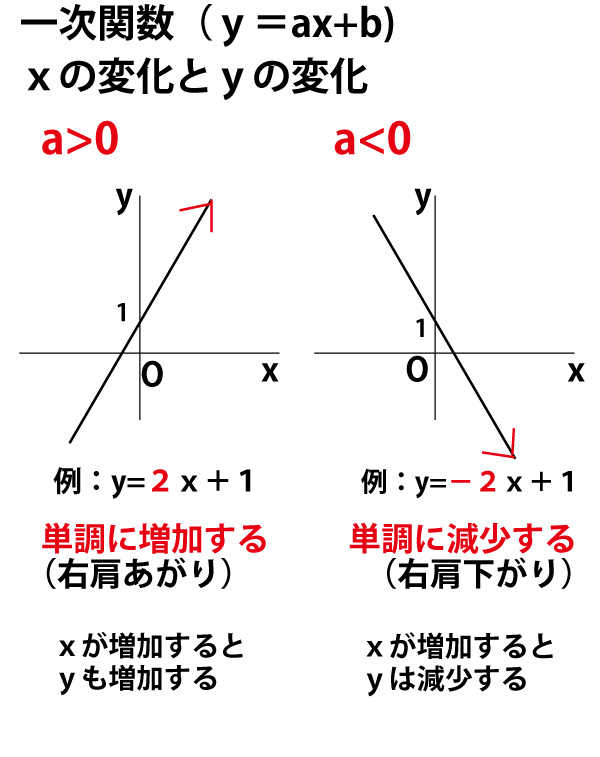
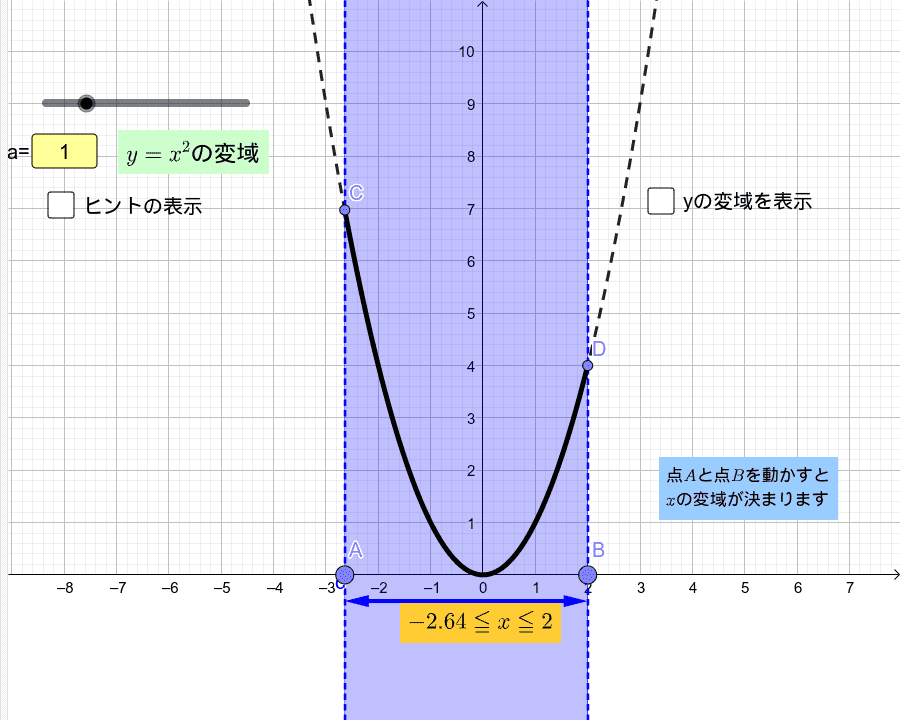
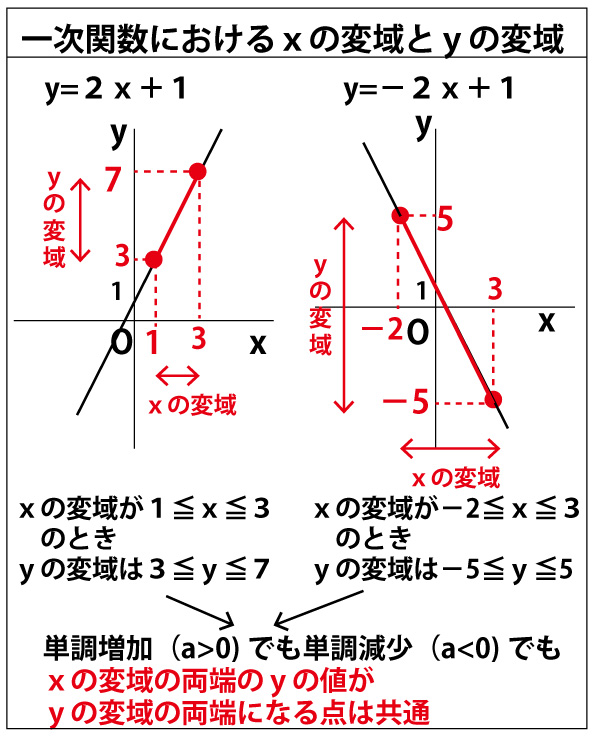
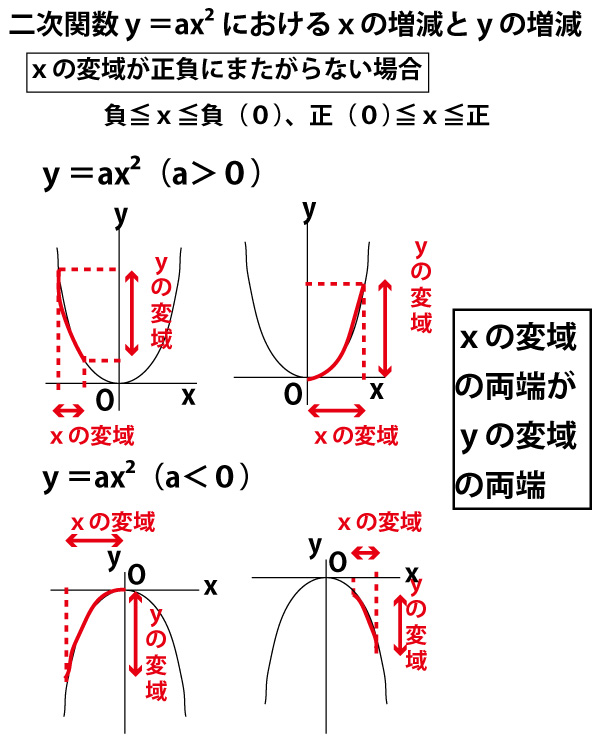
A>0の放物線y=ax 2 とm0の放物線y=ax 2 とm>0の直線y=mx16について4≦x≦8でyの変域が一致する。 aとmの値をそれぞれ求めよ。 a>0の放物線y=ax 2 とmグラフから、関数y=ax2のyの値の増減を調べること xの変域からyの変域を求めること ☆関数y=ax2のグラフをもとに、a>0の場合と同様にして、a<0の場合のyの値の増減について調べる。 小学生・中学生が勉強するならスクールTV。全国の学校の教科書に対応した動画で学習できます。
Y=ax2 グラフ 変域
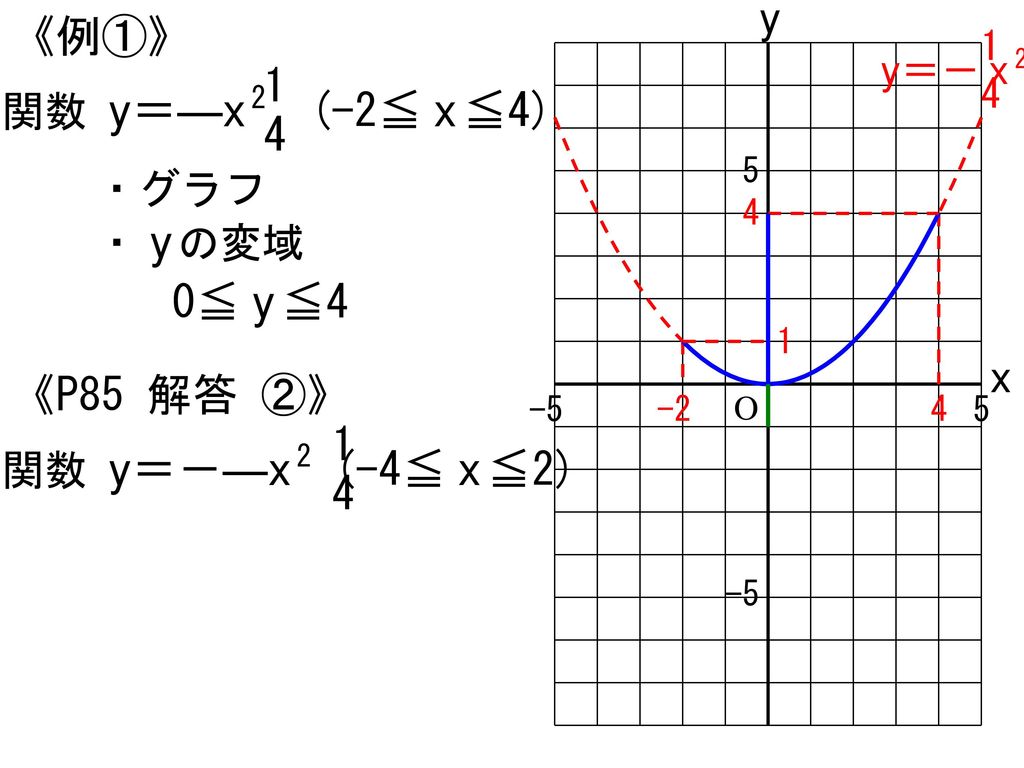
Y=ax2 グラフ 変域- 中3 y=ax二乗のグラフの性質 変域の求め方 中学生 数学のノート Clearnote 表紙 1 公開日時 16年11月05日 16時50分 更新日時 年10月日 時31分 中学生 3年生 数学関数 関数y =ax2(2) 1 次の各問いに答えなさい。 (1)yはxの2乗に比例し、x=3のときy =27である。 ① yをxの式で表しなさい。 ② x=5のときのyの値を求めなさい。 (2)関数y =ax2で,x=2のときy =−8である。 ① aの値を求めなさい。 ② x=−4のときのyの値を求めなさい。 (3)yはxの2乗に比例し,x=−2のときy =−4
2
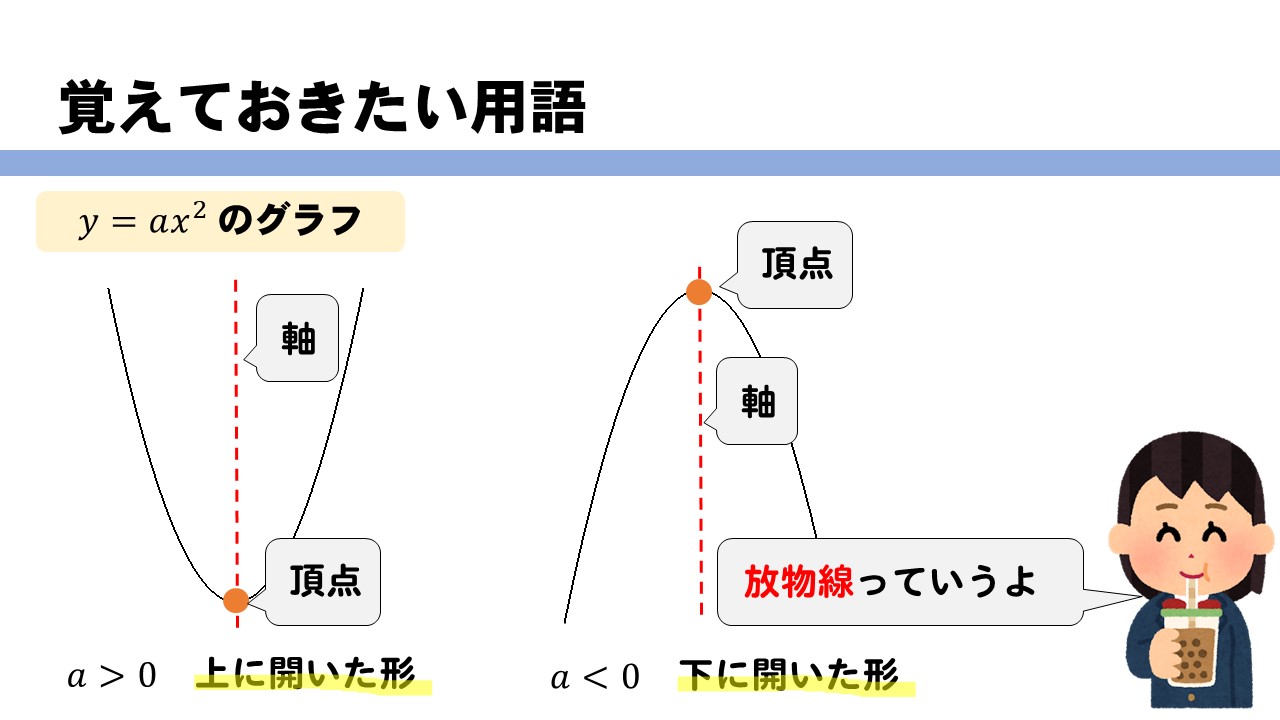
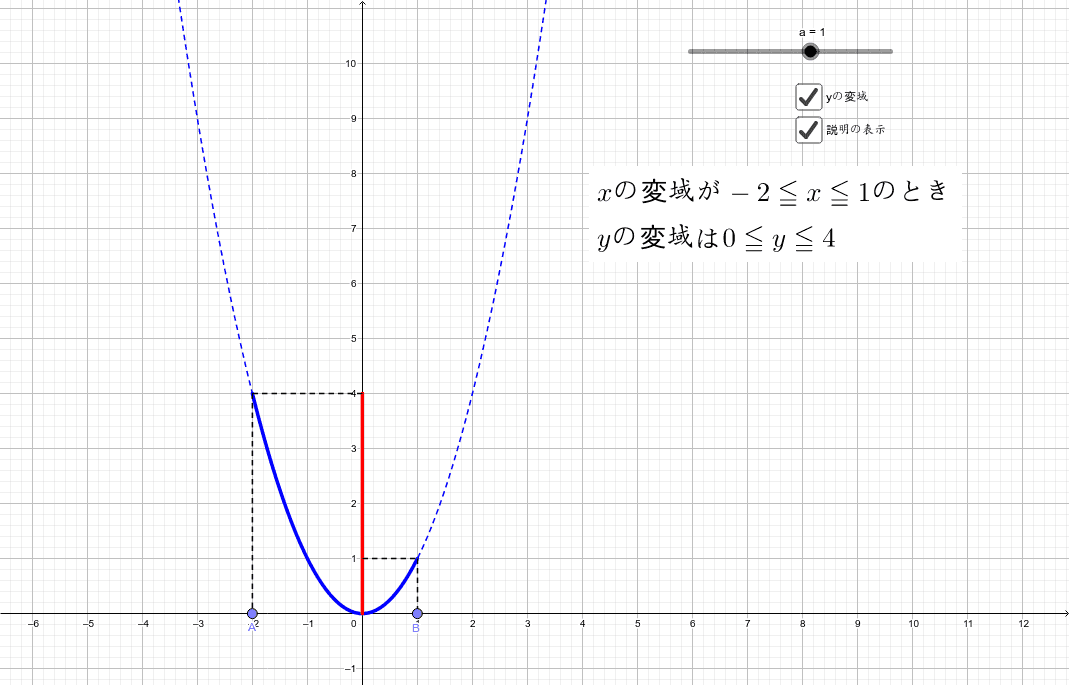
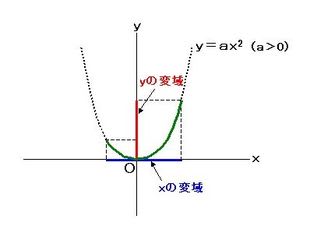
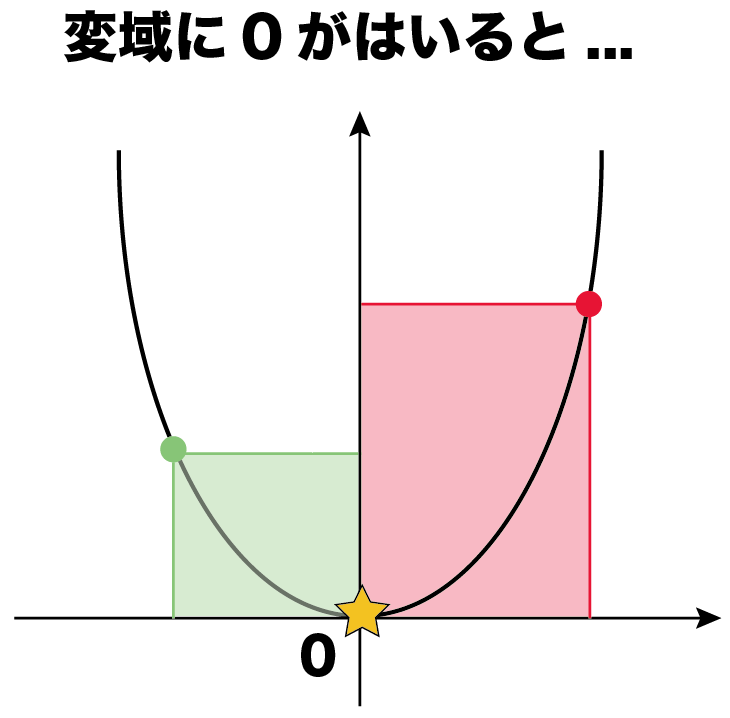
このとき,関数のグラフはその変域の部分だけを表し,残りの部分はかかないか点線で表すようにします。 比例y=axにおいて,xの変域がx 1 ≦x≦x 2 となっているとき,次のように,関数を表す式の横にxの変域をかっこの中に入れて表されることがあります。カテゴリ: @ y=ax^2(2次関数)のグラフ 高校入試 中学数学 関数 スポンサーリンク ロングコートダディ堂前透さんの出身地ということで福井県の問題を紹介していきますが,とてもとてもとても良問です。 解説するとき楽しそう。 難問だP99 1 関数y=ax2 の値の増減と変域 ひろげよう 「ひろげようをよんでください。」 「y=ax2 の値の増減についてまとめましょう。」 「a>0の場合とa<0の場合についてグラフはこういうグラフになります。」 「数学は左から右へと見ていきます。
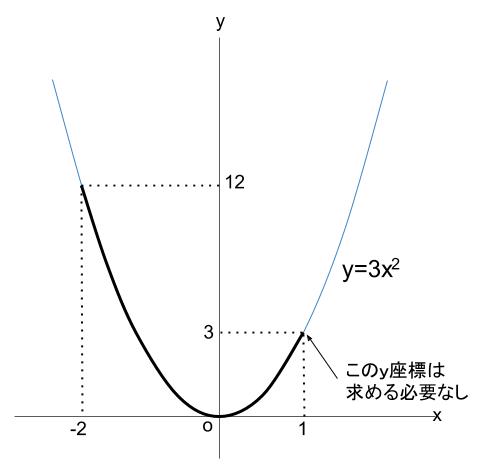
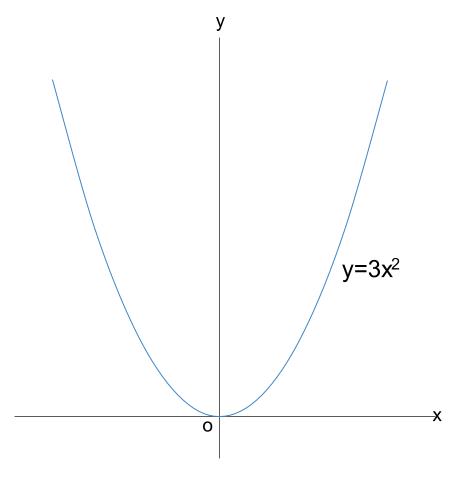
問題一括 (6,604Kb) 解答一括 (7,191Kb) 関数 y=ax 2 (2) 関数 y=ax 2 のグラフ (1) 関数 y=ax 2 のグラフ (2) 関数 y=ax 2 のグラフ (3) 関数 y=ax 2 のグラフ (4)下のグラフが\(y=3x^{2}\)です。 一方、下のグラフが\(y=3x^{2}\)です。 このように、係数\(a\)が正のときは上が開いた形に、負のときは下が開いた形となります。 より詳しく知りたい方は→中3数学y=ax^2のグラフってどんな形になるの?いくつかの特徴につい関数y=ax2の変化の割合を確認しよう! 検索 運営会社 / 利用規約
Y=ax2 グラフ 変域のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  | |
 |  |  |
「Y=ax2 グラフ 変域」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 | ||
「Y=ax2 グラフ 変域」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  |  |
「Y=ax2 グラフ 変域」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | 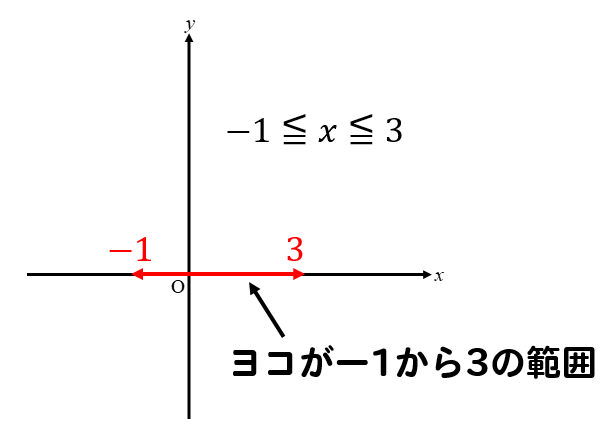 |
 | ||
「Y=ax2 グラフ 変域」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「Y=ax2 グラフ 変域」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  |  |
「Y=ax2 グラフ 変域」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | 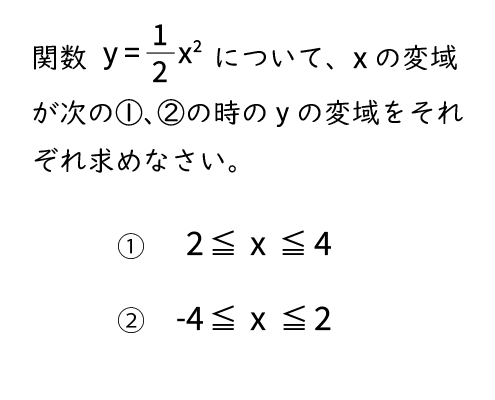 |
 |  | |
 |  | |
「Y=ax2 グラフ 変域」の画像ギャラリー、詳細は各画像をクリックしてください。
 | 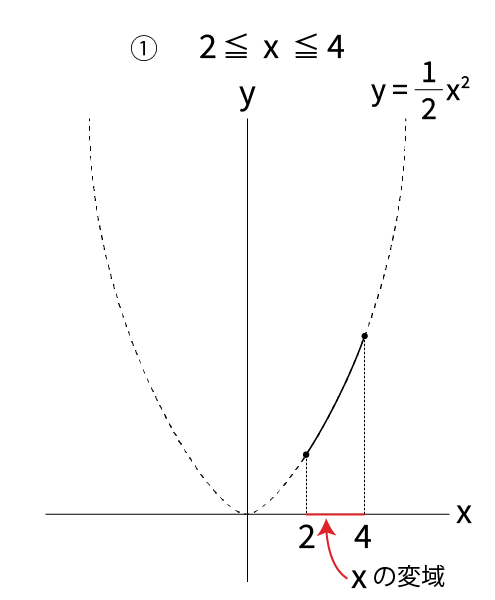 |  |
 |  | |
 | 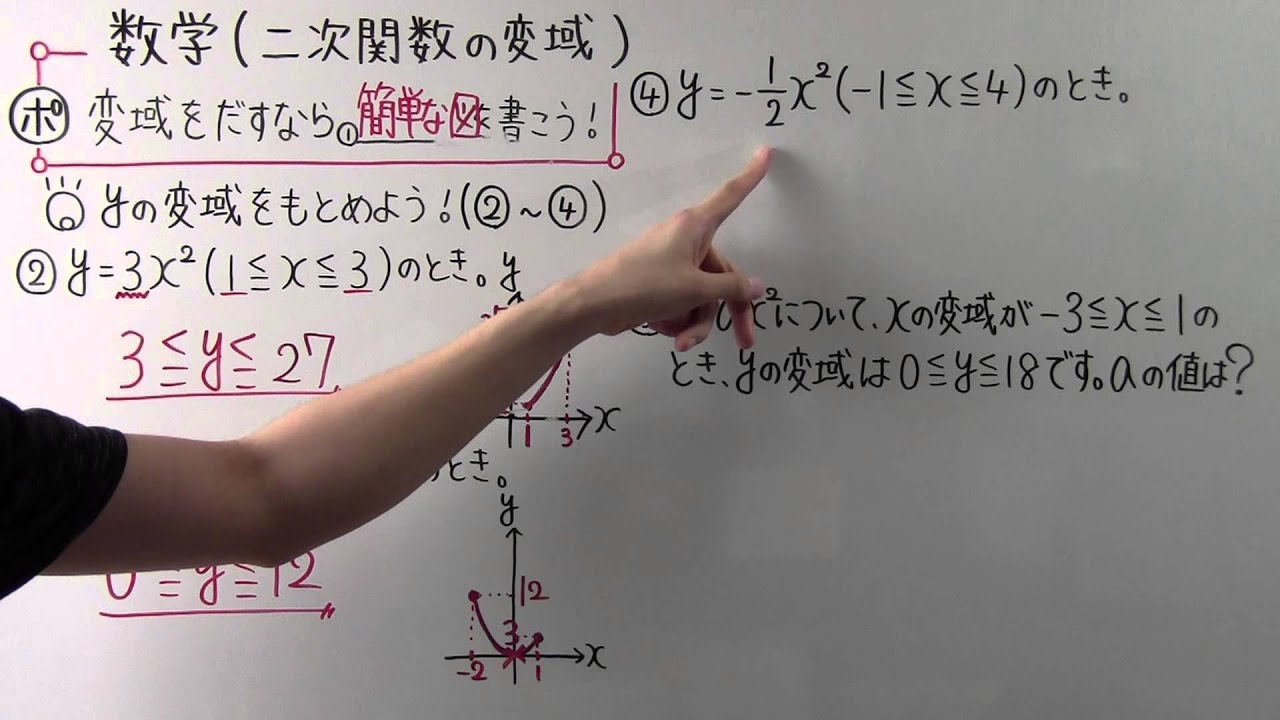 | |
「Y=ax2 グラフ 変域」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「Y=ax2 グラフ 変域」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 | ||
「Y=ax2 グラフ 変域」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 | ||
「Y=ax2 グラフ 変域」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |
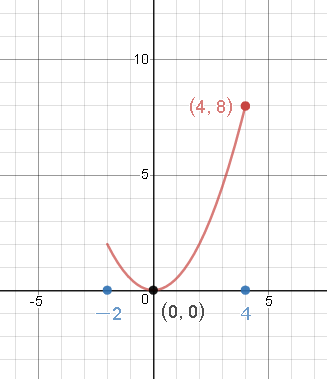
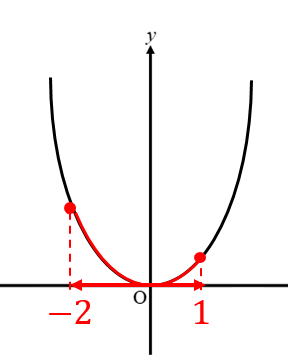
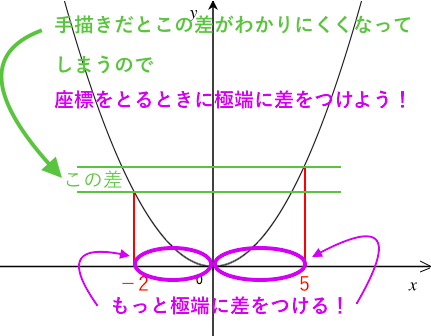
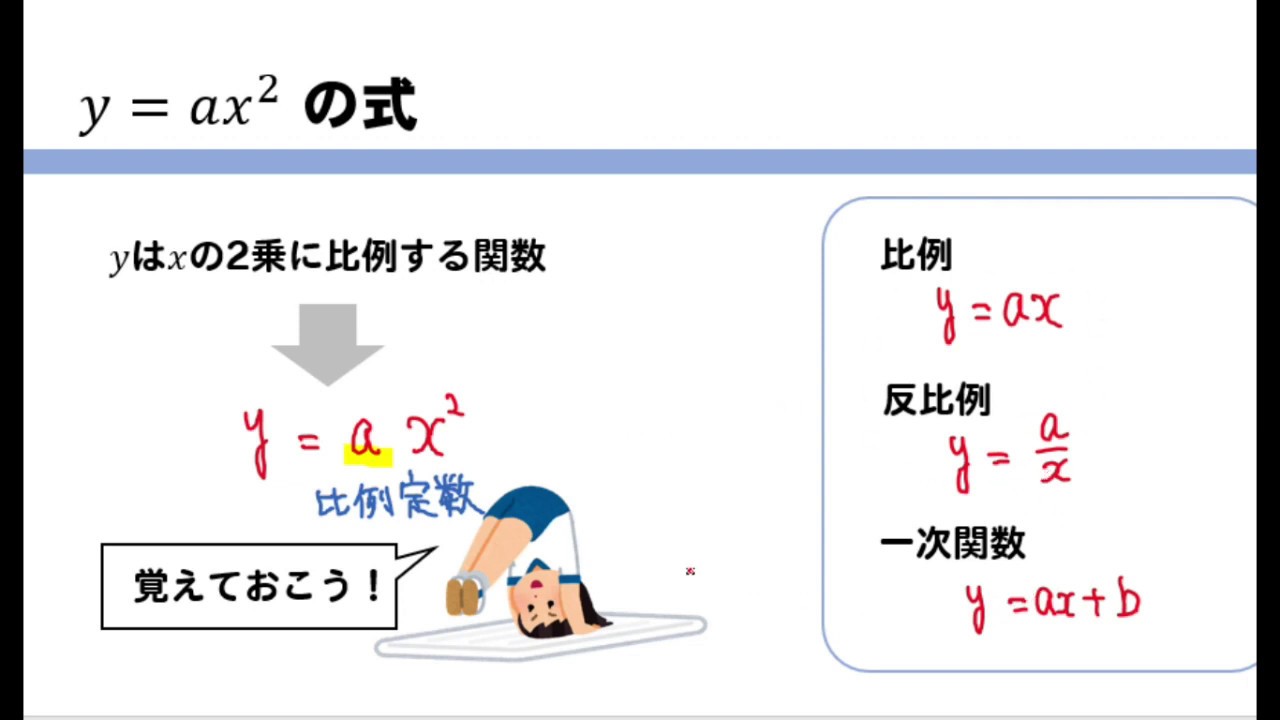
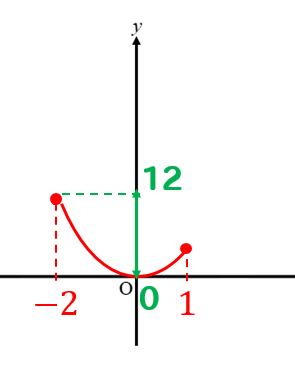
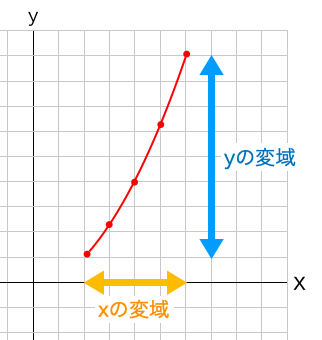
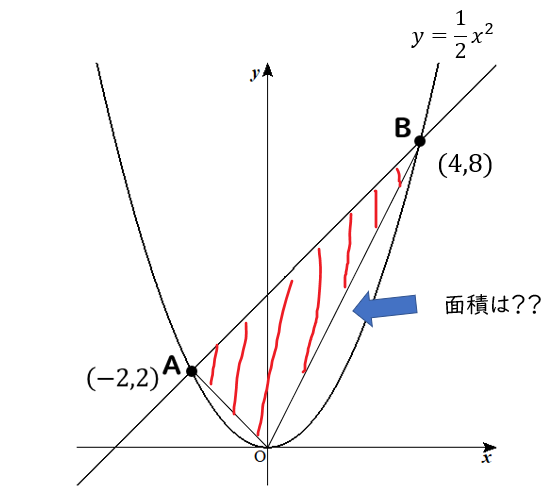
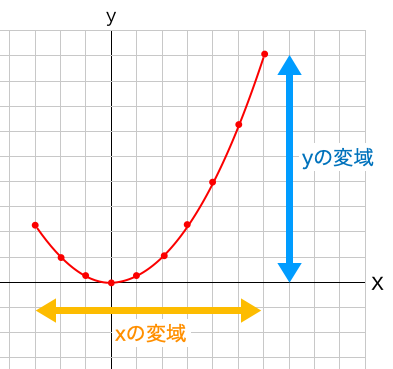
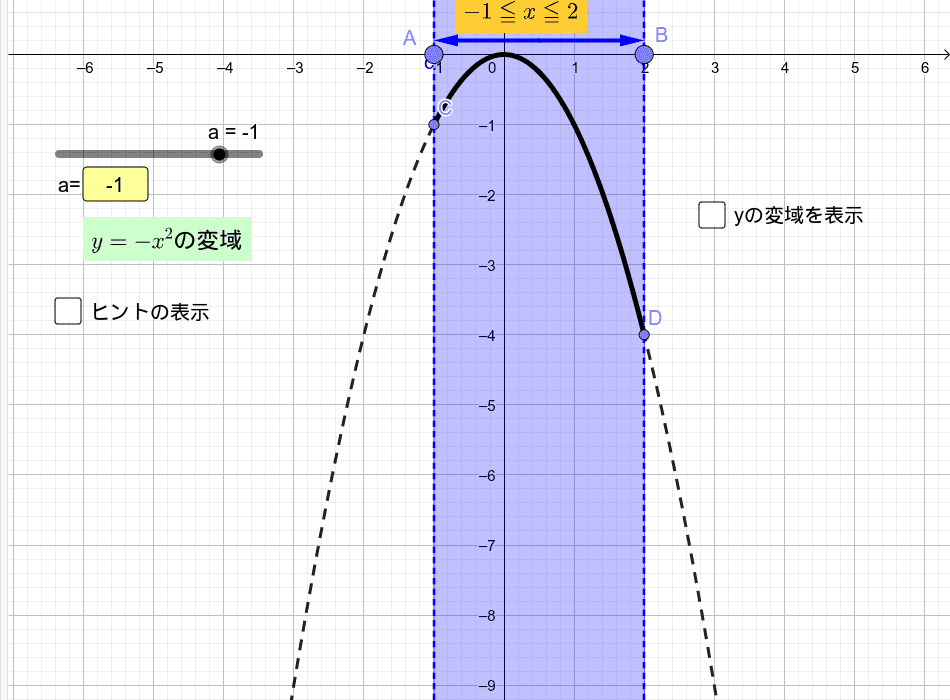
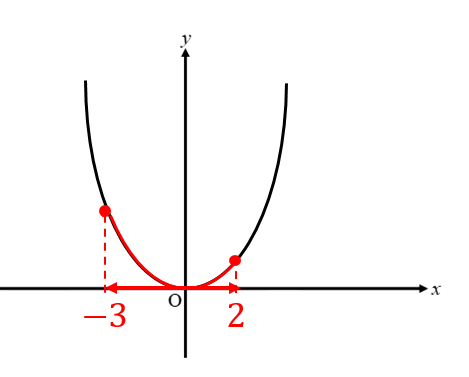
Y = ax2 y = a x 2 2乗に比例 y y が x x の関数であり、 x x と y y の間に y = ax2 y = a x 2 という関係式が成り立つとき、 y y は x x の 2 2 乗に比例する という。 ただし、 a a は 0 0 でない定数で、比例定数といいます。 「 y y は x x の 2 2 乗に比例する」と問題文に5 y=ax2 のグラフと変域(2) 関数y=ax2 について,xの変域が-1 ≦x≦2 のとき,yの変域が,b≦y≦8 となる。 このと き,a,bの値を求めなさい。 VMA06 練習問題 本問でかいたグラフを見てわかるように,xの変域を示す両端の値のx=-3,2 に対応するy の値 y=9,4 が, の変域
Incoming Term: y=ax2 グラフ 変域,
コメント
コメントを投稿